Are you wondering how mathematics has a connection to Hinduism? If yes, then we must tell you that similar to the fundamental teachings of Hinduism in the Vedas, the origins of mathematics have traced back to these ancient texts. Composed between 1500 and 900 BCE, the Vedas are historical records of human understanding and wisdom in India. Centuries ago, scholars versed in Vedic traditions wrote numerous papers and studies on mathematics. It is a prevailing and widely acknowledged viewpoint today that these writings established the groundwork for concepts like algebra, algorithms, calculating square and cube roots, various calculation techniques, and the revolutionary invention of zero.
Eurocentrism
Several scholars believe India’s contributions to science, technology, and mathematics have not achieved rightful recognition in contemporary historical narratives. They argue that several discoveries and inventions of Indian mathematicians taken by Westerners replicated these achievements and represented them as their original work. Furthermore, these scholars contend that this widespread adoption of Indian knowledge without proper acknowledgement has largely gone unnoticed due to Eurocentric biases.
Vedic Maths has many contributions to the advancements of the world. It includes Arithmetic, Geometry, Trigonometry, General Mathematics, Mathematical Logic, etc.
- Ancient Mathematics in Vedas: The Vedas, written between 1500 and 900 BCE, contain various forms of knowledge, including mathematical ideas. While they are primarily religious texts, they also include discussions related to numbers, geometric patterns, and ritual measurements. However, the mathematical content in the Vedas is not as extensive or systematic as in later texts.
- Sulba Sutras: The Sulba Sutras are a collection of ancient Indian texts that deal with various aspects of geometry, including rules for constructing sacrificial altars with precise geometric shapes. These texts are part of the larger Vedic tradition and provide practical applications of geometric concepts.
- Brahmagupta and the Concept of Zero: Brahmagupta (598–668 CE) was an Indian mathematician who made significant contributions to mathematics, including formalizing the rules for arithmetic with zero and negative numbers. His work laid the foundation for modern algebra and number theory. The concept of zero has philosophical implications in Hinduism and mathematics.
- Indian Numerals and Decimal System: The Indian numeral system, including zero, was crucial for the development of modern mathematics. These numerals eventually spread to the Arab world and Europe, leading to the decimal system we use today. This system greatly simplified arithmetic calculations and made complex mathematics more accessible.
- Influence of Hindu Cosmology: While not directly mathematical, Hindu cosmology and philosophy have influenced mathematical thought. Ideas related to infinite cycles of creation and destruction.
Baudhayana Sulba Sutra :
Pythagoras Theorem:
The Pythagorean theorem relates to the relationship between the sides of a right triangle. The Baudhayana Sulba Sutra, a part of the Yajur Veda, describes a geometric principle later formulated as the Pythagorean theorem. This ancient Indian text indicates that the square of the diagonal of a rectangle is equal to the sum of the squares of its base and height sides. It is a geometric concept similar to the Pythagorean theorem, which states:
c2 = a2+b2
where c is the hypotenuse (diagonal), and a and b are the legs of the right triangle.
दीर्घचतुरश्रस्याक्ष्णया रज्जु: पार्श्र्वमानी तिर्यग्
मानी च यत् पृथग् भूते कुरूतस्तदुभयं करोति ॥
The rope, when stretched along the length of the diagonal of a rectangle, produces an area that the vertical and horizontal sides make together.

The Baudhayana Sulba Sutra’s inclusion of this principle suggests that understanding such mathematical relationships was present in ancient Indian mathematical traditions. It’s important to note that this knowledge likely had both practical and religious significance. The Sulba Sutras were guides for constructing altars, and these constructions had to adhere to precise measurements for some rituals. Therefore, mathematical accuracy was crucial to ensure ritual success and to maintain the proper religious practices.
While the Greek mathematician Pythagoras is commonly associated with the Pythagorean theorem due to its formal proof and systematic development in ancient Greece, the principle itself was recognized and applied in various forms across different cultures and periods, including India. It highlights the interconnectedness of mathematical ideas throughout history.
Square of the root of 2:
The square root of 2 is a mathematical value, and in ancient times, there was a way to approximate it using a formula from Baudhayana and Apastamba Sulbasūtra. The written theorem is like this:
The diagonal of a square is obtained by taking the length of its sides, increasing it by one-third, then decreasing it by one-fourth of its original measure, and further adjusting it by subtracting one-thirty-fourth of this result. This formula gives an approximate value for the square root of 2.
In mathematical terms, this formula is:
2≈1+1/3+1/(3⋅4)−1/(3⋅4⋅34)=577/408≈1.4142162
This approximation is correct up to five decimal places.
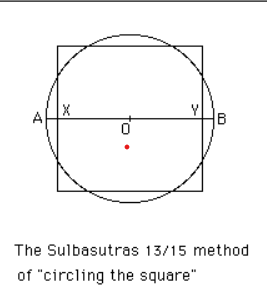
Circling the square:
Baudhayana also addressed the challenge of creating a circle with an area equal to a square. This concept is the opposite of “squaring the circle.” In his sutra i.58, he provided the following method for achieving this:
- Draw a line from the centre of the square to the midpoint of one of its sides, oriented along the East-West line.
- Next, draw a circle that includes the square but one-third of the area that extends beyond the square’s boundaries.
Infinity was known to Rishi Munis.
The idea of “infinity” was known to ancient thinkers in India, called Vedic Rishis. They understood that taking a part from infinity or adding something remains infinite. This concept is in the Isha Upanishad.
Transfinite Number:
Some specified numbers (transfinite numbers) are more than regular numbers but not the same as infinity. A long time ago, an Indian math text called Surya Prajnapti talked about three types of numbers: ones you can count, big ones, and limitless ones. They divided these into more groups.
The way we write numbers with digits and place values, like 1, 2, and 3, is also believed to have started in India. A long time ago, Indian scholars came up with the idea of using these symbols to represent numbers. They even had a way of writing numbers similar to our binary code – like a secret language made of short and long sounds.
People in ancient India also thought about numbers that could not work out exactly, like the square root of 2. They knew these kinds of numbers do not convert into simple fractions. A long time ago, an Indian thinker named Manava thought about these numbers, even before a Greek mathematician who was known for them.
Do you know how we have numbers less than zero, like -1 or -2? In some parts of the world, people used to think these were strange or not real. But in India, they understood these numbers are mandatory, especially for keeping track of money. They even wrote about how to do math with them.
In ancient India, they were good at solving problems with squares and square roots. They had methods for finding close answers to these math questions. They even solved problems that took Europe many more years to figure out.
The Vedic Rishis and other Indian mathematicians also thought about tricky math puzzles called Diophantine equations. These are about finding whole-number solutions to math problems. They created methods to solve these, and their ideas were sometimes even better than what mathematicians in other parts of the world figured out later.
Vedic Quadratic Equations
During ancient times in India, specifically in the 8th century BC, the Sulba Sutras says that quadratic equations of type ax^2 = c and ax^2 + bx = c, using geometric techniques. Similarly, Babylonian mathematicians around 400 BC, Chinese mathematicians around 200 BC, and the Greek mathematician Euclid around 300 BC solve quadratic equations with positive solutions. They did not possess a general formula. Then, in 628 AD, an Indian mathematician named Brahmagupta provided the first solution to the quadratic equation ax^2 + bx = c.
The Bakhshali Manuscript, created in India during the 7th century AD, contained an algebraic formula for solving quadratic equations, quadratic indeterminate equations of the form ax/c = y.
The knowledge of the Fibonacci sequence was prevalent in ancient India, where it found applications in metrical sciences like prosody. This understanding predates its recognition in Europe. Its origins have links to individuals such as Pingala (around 200 BCE), Virahanka (6th century CE), Gopāla (circa 1135 CE), and Hemachandra (circa 1150 CE). In the Western world, Fibonacci, also known as Leonardo of Pisa, studied the sequence in his work “Liber Abaci” (1202). The serial is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.
List of Indian Mathematical Inventions and Foreign Claims:
- Mahavira Formula (850 AD): A formula for combinations, nCr = (n)! / (r!) (n-r)! where ‘!’ denotes factorial.
- Bhaskaracharya (1114-1193): Contributions include Rolle’s theorem (1652-1719) and a formula for relative difference related to retrograde motion.
- Madhav’s theorem (1340-1425) Stated the Gregory Series (1638-1675), a formula involving a series of tangent terms.
- Madhav’s Series (1340-1425): Derived a series for calculating the value of π (pi): II = 1 – 1/3 + 1/5 – 1/7 + …
- Narayan Pandit (1356 AD): Developed a factorization method for finding divisors of a number.
- Bhaskaracharya (1114-1193): Euler’s division algorithm, a method for finding the greatest common divisor.
- Permeshwara (1360 AD): Developed a formula for finding the circum-radius of a cyclic quadrilateral.
- Nilkanth Somyaji (1444-1545): He presented summation formulas for sequences involving n, n^2, and n^3.
- Nilkanth Somyaji (1444-1545): Contributed to Euler’s results, particularly the r sine rule involving the sides and angles of a triangle.
- Brahmagupta (628 AD): He discovered formulas for calculating volumes of a frustum of a cone and a pyramid.
- Jyeshtha Deo (1500 AD): He presented formulae for sin(x+y) and cos(x+y) in Yuktibhasha.
- Jyeshtha Deo (1500 AD): Worked on linear equations, similar to Leibnitz (1646-1716).
- Jyeshtha Deo (1500 AD): He formulated volumes and surface area of a sphere using integration, akin to Leibnitz.
- Shankar Variar (1500-60): He calculated values related to π (pi) similar to Gauss (1777-1855).
The list highlights Indian mathematicians who developed various mathematical concepts and methods before their foreign counterparts. These contributions have a significant role in the need for more research to restore recognition to these forgotten Indian mathematicians.



